LIBERDADE PARA O RACIOCÍNIO

A tentativa de acomodar hóspedes num hotel lotado, porém com infinitos quartos, pode ser um ótimo exercício para a mente.

Há quem considere que frente a um problema novo (sem um método de resolução previsto na literatura matemática ou cuja solução não admita analogias com os processos conhecidos), duas pessoas igualmente inteligentes têm as mesmas chances de chegar a um resultado.  Mesmo que uma tenha formação matemática e a outra não.  Há quem diga até que o não-matemático pode ser mais rápido, uma vez que pensa livremente, enquanto o outro varre, ainda que inconscientemente, a lista dos métodos aprendidos durante seu treinamento.

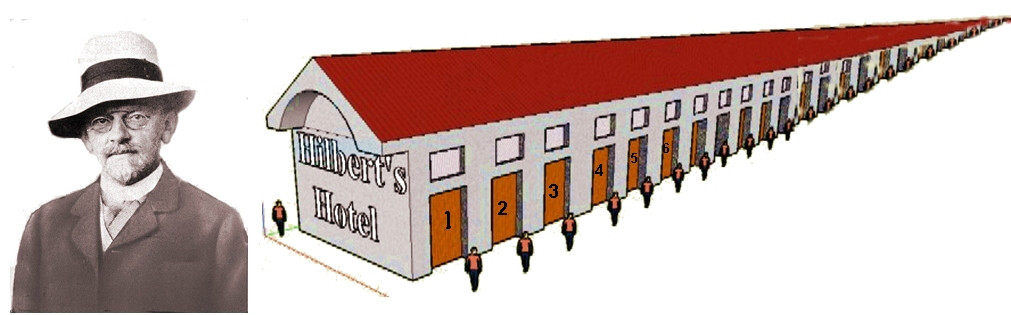
Alguém que levasse ao extremo tais considerações poderia imaginar que o melhor método pedagógico na solução de problemas talvez fosse o de não ensinar nenhum dos procedimentos clássicos.  Uma tolice, como qualquer educador experimentado sabe.  Mas, apesar de tudo, a escolha de currículos adequados não tem se mostrado tarefa fácil ou óbvia. Uma coisa é treinar crianças para executar rotinas preestabelecidas, outra é exercita-las para uma ação libertadora do raciocínio.  Parece não haver dúvidas de que praticar métodos criativos, com os quais os homens de gênio já resolveram grandes enigmas, é um excelente jogging para o cérebro, em especial na juventude.  Coisa que eu pude constatar recentemente, quando visitava um museu na Austrália.  Havia lá um setor no qual as crianças realizavam experimentos, montavam protótipos, buscavam soluções mais adequadas para aparelhos que consomem energia, entre outras atividades.  Num canto, numa “barraca do infinito”, um monitor brincava com as crianças.  “Um hotel tem uma infinidade de quartos assim numerados:  1, 2, 3, 4, 5 etc”, dizia ele.  “No final da tarde chega um hóspede e ouve do porteiro a desagradável informação de que a casa está lotada.  Mas o gerente interfere e diz que não há problema, pois o hóspede do quarto 1 pode ir para o de número 2, o do 2 para o 3, o do 3 para o 4 e assim por diante, de modo que o recém-chegado possa ocupar o quarto número 1.”

Mesmo para as disciplinadas crianças australianas a história foi demais.  “Ora, se o hotel está lotado, alguém tem de sair para que o novo hóspede ocupe o quarto número 1”, disse um dos garotos.  “Quem?”, perguntou o monitor.  E aí a coisa complicou.  Se o 1 vai para o 2, o 2 para o 3 e assim por diante, acabará sobrando para o hóspede do último quarto.  Mas qual é o último número natural?  Aos poucos as crianças foram se dando conta de que em conjuntos infinitos como o dos números naturais aparecem algumas propriedades impensáveis para os conjuntos finitos.  Logo um dos meninos falou:  “Mesmo que venham vinte novos hóspedes para o hotel lotado, basta eu transferir o do quarto 1 para o 21, o do 2 para o 22 e assim por diante.”  O professor concordou:  “Certo, e se chegassem 1.000, o do quarto 1 iria para o 1.001, o do 2 para o 1.002 etc, até que todos pudessem ser acomodados nos 1.000 primeiros quartos”.  Na verdade, mesmo que aparecesse uma infinidade de novos hóspedes haveria como acomoda-los num hotel com um número infinito de quartos.  Bastaria mandar o hóspede do quarto 1 para o 2 o do 2 para o 4, o do 3 para o 6 e assim por diante.  Vão sobrar os infinitos quartos numerados por 1, 3, 5, 7, 9, 11, 13 etc, suficientes para alojar a infinidade de novos hós

Deve-se esta história curiosa ao matemático alemão David Hilbert (1862-1943).  Embora sua contribuição seja um monumento, Hilbert usou a alegoria para ilustrar ideias de outro matemático alemão, Geog Cantor (1845-1918), autor de  Contribuições à Fundamentação da Teoria dos Conjuntos Transfinitos.  Cantor também mostrou que o conjunto dos números racionais positivos (isto é, das velhas frações 5/2, ¾ etc) pode ser colocado em correspondência um a um com o conjunto dos números naturais {1, 2, 3, 4, ...}.  Fiquei imaginando que aquele monitor do museu certamente teria um jeito lúdico e criativo para ilustrar tal proposição, mesmo que fosse para um público mais velho.  E seus ouvintes, ao entrar em contato de um modo divertido com ideias tão pouco comuns, sem dúvida teriam (como terão os garotos que ouviram a história do hotel) maior prontidão para estudar assuntos delicados.

Por Luiz Barco/Super